LP[線性規劃英文縮寫]

線性規劃（Linear programming,簡稱LP）是運籌學中研究較早、發展較快、套用廣泛、方法較成熟的一個重要分支，它是輔助人們進行科學管理的一種數學方法。研究線性約束條件下線性目標函式的極值問題的數學理論和方法。英文縮寫LP。它是運籌學的一個重要分支，廣泛套用于軍事作戰、經濟分析、經營管理和工程技術等方面。為合理地利用有限的人力、物力、財力等資源作出的最優決策，提供科學的依據。

基本信息

• 中文名稱：線性規劃
• 外文名：linear programming
• 學科門類：運籌學
• 研究範圍：線性最最佳化問題

• 套用學科：高中數學必修5

線性規劃簡介

數學模型

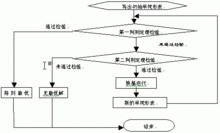線性規劃步驟

（1）列出約束條件及目標函式

（2）畫出約束條件所表示的可行域

（3）在可行域內求目標函式的最優解及最優值

標準型

描述線性規劃問題的常用和最直觀形式是標準型。標準型包括以下三個部分：

一個需要極大化的線性函式：

lp[線性規劃英文縮寫]

lp[線性規劃英文縮寫]

lp[線性規劃英文縮寫]

lp[線性規劃英文縮寫]

以下形式的問題約束：

lp[線性規劃英文縮寫]

lp[線性規劃英文縮寫]

和非負變數：

其他類型的問題，例如極小化問題，不同形式的約束問題，和有負變數的問題，都可以改寫成其等價問題的標準型。

模型建立

從實際問題中建立數學模型一般有以下三個步驟；

1.根據影響所要達到目的的因素找到決策變數；

2.由決策變數和所在達到目的之間的函式關係確定目標函式；

線性規劃難題解法

3.由決策變數所受的限制條件確定決策變數所要滿足的約束條件。

所建立的數學模型具有以下特點：

1、每個模型都有若干個決策變數（x1，x2，x3……，xn），其中n為決策變數個數。決策變數的一組值表示一種方案，同時決策變數一般是非負的。

2、目標函式是決策變數的線性函式，根據具體問題可以是最大化（max）或最小化（min），二者統稱為最最佳化（opt）。

3、約束條件也是決策變數的線性函式。

當我們得到的數學模型的目標函式為線性函式，約束條件為線性等式或不等式時稱此數學模型為線性規劃模型。

例：

生產安排模型：某工廠要安排生產Ⅰ、Ⅱ兩種產品，已知生產單位產品所需的設備台時及A、B兩種原材料的消耗，如表所示，表中右邊一列是每日設備能力及原材料供應的限量，該工廠生產一單位產品Ⅰ可獲利2元，生產一單位產品Ⅱ可獲利3元，問應如何安排生產，使其獲利最多？

解：

1、確定決策變數：設x1、x2分別為產品Ⅰ、Ⅱ的生產數量；

2、明確目標函式：獲利最大，即求2x1+3x2最大值；

3、所滿足的約束條件：

設備限制：x1+2x2≤8

原材料A限制：4x1≤16

原材料B限制：4x2≤12

基本要求：x1，x2≥0

用max代替最大值，s.t.（subject to 的簡寫）代替約束條件，則該模型可記為：

max z=2x1+3x2

s.t. x1+2x2≤8

4x1≤16

4x2≤12

x1，x2≥0

解法

求解線性規劃問題的基本方法是單純形法，已有單純形法的標準軟體，可在電子計算機上求解約束條件和決策變數數達 10000個以上的線性規劃問題。為了提高解題速度，又有改進單純形法、對偶單純形法、原始對偶方法、分解算法和各種多項式時間算法。對於只有兩個變數的簡單的線性規劃問題，也可採用圖解法求解。這種方法僅適用於只有兩個變數的線性規劃問題。它的特點是直觀而易於理解，但實用價值不大。通過圖解法求解可以理解線性規劃的一些基本概念。

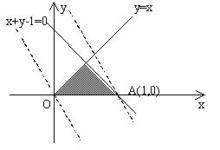圖解法解線性規劃問題

對於一般線性規劃問題：Min z=CX

S.T.

AX =b

X>=0

其中A為一個m*n矩陣。

若A行滿秩

則可以找到基矩陣B，並尋找初始基解。

用N表示對應於B的非基矩陣。則規劃問題1可化為：

規劃問題2：

Min z=CB XB+CNXN

線性規劃法解題

S.T.B XB+N XN = b (1)

XB >= 0, XN >= 0 (2)

(1)兩邊同乘於B-1，得

XB + B-1 N XN = B-1 b

同時，由上式得XB = B-1 b - B-1 N XN，也代入目標函式，問題可以繼續化為：

規劃問題3：

Min z=CB B-1 b + ( CN - CB B-1 N ) XN

S.T.

XB+B-1N XN = B-1 b (1)

XB >= 0, XN >= 0 (2)

令N:=B-1N，b:= B-1 b，ζ= CB B-1b，σ= CN - CB B-1 N，則上述問題化為規劃問題形式4：

Min z= ζ + σ XN

S.T.

XB+ N XN = b (1)

XB >= 0, XN >= 0 (2)

在上述變換中，若能找到規劃問題形式4，使得b>=0，稱該形式為初始基解形式。

上述的變換相當於對整個擴展矩陣（包含C及A） 乘以增廣矩陣 。所以重在選擇B，從而找出對應的CB。

若存在初始基解

若σ>= 0

則z >=ζ。同時，令XN = 0，XB = b，這是一個可行解，且此時z=ζ，即達到最優值。所以，此時可以得到最優解。

若σ >= 0不成立

可以採用單純形表變換。

σ中存在分量0。

l βq+βi*(-aq,j/ai,j)>=0，其中q!=i。即βq>=βi/ ai,j * aq,j。

n 若aq,j0，則需要βq / aq,j >=βi/ ai,j。因此，要選擇i使得βi/ ai,j最小。

如果這種方法確定了多個下標，選擇下標最小的一個。

轉換後得到規劃問題4的形式，繼續對σ進行判斷。由於基解是有限個，因此，一定可以在有限步跳出該循環。

若對於每一個i，ai,j